C++ Компьютерная графика

Построить изображение поверхности z=f(x,y) в параллельной проекции ex = y – 0.7 x, ey = z – 0.7 x.

Задание
Разработать программу на языке программирования Borland C++  Builder для вывода на экран изображения поверхности с удалением невидимых линий.
Введение
В данной работе отражен вывод на экран изображения поверхности в среде программирования Borland С++ Builder 6 Enterprise.

Построить изображение поверхности

z=f(x,y)

в параллельной проекции

ex=y-0,7x

,

ey=z-0,7x

.

//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include <math.h>
#include "rgz03.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
#include <stdlib.h>
#include <math.h>
#define nx 100
#define ny 100

int algor=1;
float xmax = 3, xmin = -3, ymax = 3, ymin = -3,  zmax = 3, zmin = -2,hx,hy;
float xv = 50, yv = 30.5 , zv = 10 ; // положение наблюдателя
float d = 1,zz=0.2 ;            // расстояние до плоскости проекции
float cosa, sina ;         // меридиана точки наблюдения
float exmax, exmin, eymax, eymin ;
int gmex, gmey ;
int *phimin, *phimax ;
float cvals[ny+1], cval ;

void line(int x0, int y0, int x1, int y1){
        Form1->Image1->Canvas->MoveTo(x0,y0);
        Form1->Image1->Canvas->LineTo(x1,y1);
}

void sline( int x0, int y0, int x1, int y1 ){
int i,j, temp, x, y, maxacc, accx, accy, dx, dy,
            length=abs(x1-x0);
     if ((i=abs(y1-y0))>length) length=i;
//     if (length==0) return;
     maxacc=2*length; accx=accy=length;
    for (j=0; j<2; j++){
      dx=2*(x1-x0); dy=2*(y1-y0); x=x0; y=y0;
        length+=j;
      for (i=0; i<length; i++){
                              if (y0<=y1&&phimax[x]<y){
                        Form1->Image1->Canvas->Pixels[x][gmey-y]=clBlack;
                        phimax[x]=y;
            }
            if (y0>=y1&&phimin[x]>y){
                        Form1->Image1->Canvas->Pixels[x][gmey-y]=clBlack;
                        phimin[x]=y;
            }
            accx+=dx; accy+=dy;
            if (accx>=maxacc){
                accx-=maxacc; x++;
            } else if (accx<0){
                  accx+=maxacc; x--;
              }
            if (accy>=maxacc){
                  accy-=maxacc; y++;
            } else if (accy<0){
                  accy+=maxacc; y--;
              }
      }
      temp=x0; x0=x1; x1=temp; temp=y0; y0=y1; y1=temp;
     }
}

float fz(float x, float y) {return ((x*y)/(x*x+y*y))*zz;}

float ex(float x, float y, float z){
 return y-0.5*x;
}

float ey ( float x, float y, float z ){
 return z-2*x;
}

void vectphi(float x0, float y0, float z0,
float x1, float y1, float z1,int mm){
float ex0, ex1, ey0, ey1;
int ix0, ix1, iy0, iy1;
     ex0=ex(x0,y0,z0);
     ix0=(ex0-exmin)*gmex/(exmax-exmin);
     ey0=ey(x0,y0,z0);
     iy0=(ey0-eymin)*gmey/(eymax-eymin);
     ex1=ex(x1,y1,z1);
     ix1=(ex1-exmin)*gmex/(exmax-exmin);
     ey1=ey(x1,y1,z1);
     iy1=(ey1-eymin)*gmey/(eymax-eymin);
     if (mm) sline(ix0,iy0,ix1,iy1);
      else line(ix0,gmey-iy0,ix1,gmey-iy1);
}
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
        : TForm(Owner){
int i, j;
float x,y,z;
  hy=(ymax-ymin)/ny;
  hx=(xmax-xmin)/nx;
  gmex=Form1->Image1->Width;
  gmey=Form1->Image1->Height;
  cosa=xv/sqrt(xv*xv+yv*yv);
  sina=yv/sqrt(xv*xv+yv*yv );
}
//---------------------------------------------------------------------------

void __fastcall TForm1::Button1Click(TObject *Sender){
zz+=0.1;
int i,j; float x, y, z;
  Form1->Image1->Canvas->FillRect(TRect(0,0,gmex,gmey));
  zmin=zmax=0.;
  for (i=0; i<=nx; i++)
  for (j=0; j<=ny; j++){
   z=fz(xmin+i*hx,ymin+j*hy);
   if (z>zmax) zmax=z;
   if (z<zmin) zmin=z;
}
 exmax=ex(xmin, ymax, zmax);
  exmin=ex(xmax, ymin, zmin);
  eymax=ey(xmin, ymin, zmax);
  eymin=ey(xmax, ymax, zmin);
  for(x=xmin; x<=xmax; x+=xmax-xmin)
  for(y=ymin; y<=ymax; y+=ymax-ymin)
  for(z=zmin; z<=zmax; z+=zmax-zmin){
        if (exmax<ex(x,y,z)) exmax=ex(x,y,z);
        if (exmin>ex(x,y,z)) exmin=ex(x,y,z);
        if (eymax<ey(x,y,z)) eymax=ey(x,y,z);
        if (eymin>ex(x,y,z)) eymin=ey(x,y,z);
  }
 phimax=new int[gmex]; phimin=new int[gmex];
    for(i=0;i<gmex;i++) {phimax[i]=0; phimin[i]=gmey;}
    cval=fz(xmax, ymax);
    for(i=ny-1;i>=0;i--){
        cvals[i+1]=cval; y=ymin+hy*i;
        cval=fz(xmax, y);
        vectphi(xmax, y+hy, cvals[i+1], xmax, y, cval, 1);
    }
    cvals[0] = cval ;
    for (j=nx-1;j>=0;j--){
        x=xmin+hx*j;
        cval=fz(x, ymax);
        vectphi(x+hx, ymax, cvals[ny], x,ymax,cval, 1);
        for(i=ny-1;i>=0;i--){
                cvals[i+1]=cval; y=ymin+hy*i;
              cval=fz(x, y);
                vectphi(x+hx, y, cvals[i], x, y, cval, 1);
                vectphi(x, y+hy, cvals[i+1], x, y, cval, 1);
        }
        cvals[0] = cval ;
    }
    vectphi(xmax, ymax, zmax, xmin, ymax, zmax, 0);
    vectphi(xmax, ymax, zmax, xmax, ymax, zmin, 0);
    vectphi(xmax, ymax, zmax, xmax, ymin, zmax, 0);
    vectphi(xmin, ymax, zmin, xmin, ymax, zmax, 0);
    vectphi(xmin, ymax, zmin, xmax, ymax, zmin, 0);
    vectphi(xmax, ymin, zmin, xmax, ymin, zmax, 0);
    vectphi(xmax, ymin, zmin, xmax, ymax, zmin, 0);
    vectphi(xmin, ymin, zmin, xmin, ymin, zmax, 1);
    vectphi(xmin, ymin, zmin, xmax, ymin, zmin, 1);
    vectphi(xmin, ymin, zmin, xmin, ymax, zmin, 1);
    vectphi(xmax, ymin, zmax, xmin, ymin, zmax, 1);
    vectphi(xmin, ymax, zmax, xmin, ymin, zmax, 1);
    delete phimax; delete phimin;
}

Программная реализация с использованием алгоритма плавающего горизонта показана на рисунке 1.

C++ Компьютерная графика

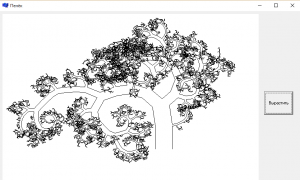
Построить дерево Аммерала

Задание
Построить дерево Аммерала.

В данной работе отражен вывод дерева Аммерала в среде программирования Borland С++ Builder 6 Enterprise. А так же разработка исходного кода вывода функции.

Пояснение. Идея алгоритма построения дерева принадлежит Аммералу. Сначала выводится прямоугольник, соответствующий стволу дерева. Затем на верхней стороне прямоугольника строится прямоугольный треугольник, для которого эта сторона служит гипотенузой. Затем на каждом из катетов полученного прямоугольного треугольника будут построены прямоугольники, и этот процесс будет рекурсивно применен к каждому из этих двух прямоугольников.

//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include <math.h>
#include "rgz2zd2.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
        : TForm(Owner)
{
}
//---------------------------------------------------------------------------
float xmin=-400, xmax=800; // масштаб по x
float ymin=200, ymax=1300; //мастштаб по у
const double PI=3.14159;
int maxX, maxY, zz=0;
float xdens, ydens;
int ex(float x){
	return (int) ((x-xmin)/xdens);
}
int ey(float y){
	return (int) ((ymax-y)/ydens);
}
//вывод отрезка
void line(int x0, int y0,int x1, int y1){
        Form1->Image1->Canvas->MoveTo(x0,y0);
        Form1->Image1->Canvas->LineTo(x1,y1);
}

// рекурсивная функция построения дерева
void piphagor(float x0,float y0,float x1, float y1){
	float x0s, y0s, x1s, y1s, x2s, y2s;
	float lambda= 1.+(2.-1.)*(0.+rand()%10000)/10000;
	float phi= PI/2 + (PI-PI/2)*(0.+rand()%10000)/10000;
	if((x1-x0)*(x1-x0)+(y1-y0)*(y1-y0)<1){
			line(ex(x0),ey(maxY-y0),ex(x1),ey(maxY-y1));
			return;
	}
	x0s= x0-lambda*(y1-y0); y0s= y0+lambda*(x1-x0);
	x1s= x1-lambda*(y1-y0); y1s= y1+lambda*(x1-x0);
     	line(ex(x0), ey(maxY-y0), ex(x0s), ey(maxY-y0s));
	line(ex(x1), ey(maxY-y1), ex(x1s), ey(maxY-y1s));
	x2s= (x0s+x1s)/2+ (x1s-x0s)/2*cos(phi)-(y1s-y0s)/2*sin(phi);
	y2s= (y0s+y1s)/2+ (x1s-x0s)/2*sin(phi)+(y1s-y0s)/2*cos(phi);
	piphagor(x0s,y0s,x2s,y2s);
	piphagor(x2s,y2s,x1s,y1s);
}

void __fastcall TForm1::trolo(TObject *Sender){
Form1->Image1->Picture->Bitmap->FreeImage();
Form1->Image1->Picture->Bitmap = NULL;
maxX=Form1->Image1->Width;
maxY=Form1->Image1->Height;
xdens=(xmax-xmin)/maxX;
ydens=(ymax-ymin)/maxY;
piphagor(maxX/2+40, 0, maxX/2-40, 0);
}

Вывод построенного дерева показан на рисунке 1.

Новости

Обновление сайта

Всем здрасти.
Сайт получил новое глобальное обновление.
Ключевая идея заключается в том что теперь все могут писать свои посты и этим помогать людям.
Теперь сайт нормально отображает формулы и исходные коды

if(result <= 0.0 && result >=0.0){//Do some code}

Поиск был доработан, теперь искать посты можно в связке с несколькими тегами.
Ну и множество более мелких изменений для удобства пользователей.

параллельное программирование C++

Разработать программу, загружающую два параллельно работающих процесса, выводящих в свои окна указанные графические данные

Задание1: Параллельные процессы
Разработать программу, загружающую два параллельно работающих
процесса, выводящих в свои окна указанные графические данные

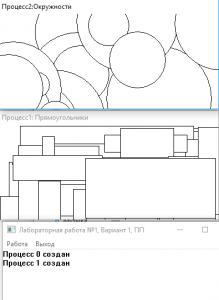
Окружность и прямоугольник

Область вывода состоит из двух окон: верхнего и нижнего в нечетных
вариантах или левого и правого в четных вариантах. Каждый процесс выводит в свое окно фигуры заданного вида, у которых случайно изменяются цвет,
размеры и положение.

Задание 2: Распараллеливание рекурсивных подпрограмм

Разработать программу, решающую данную задачу с помощью
рекурсивной функции. Преобразовать эту функцию и главную программу в много потоковуюпрограмму. Потоковые функции выполняются со случайной задержкой.

Вариант 1: Вычисление значений многочлена по схеме
Горнера методом сдваивания.



Исходный код программы:
Первый процесс:

#include <windows.h>	//заголовочный файл для win32 приложений
#pragma hdrstop
#define SizeWindow 400	//размер окна

MSG msg;		//сообщение
HDC hdc;		//контекст устройства
HBRUSH hBrush;		//тип кисти
HWND Wnd;		//handle окна
WNDCLASS wnds;		//структура класса окна
char ClassName[255]="Rectangle";	//имя класса окна

LRESULT CALLBACK WindowProc(HWND hWnd, UINT uMsg, WPARAM wParam, LPARAM lParam){//оконная функция
switch(uMsg) //обработчик сообщений
{ 		
	case WM_DESTROY:		//выход
		PostQuitMessage(0); return 0;
	case WM_TIMER:		//сработал таймер и нарисовали произвольный четырёхугольник
		Rectangle(hdc, rand() %SizeWindow, rand()%SizeWindow/2, rand()%SizeWindow, rand()%SizeWindow); //нарисовали произвольный четырёхугольник
	default:			//по умолчанию 
		DefWindowProc(hWnd, uMsg, wParam, lParam);
		break;
}
}

int WinMain(HINSTANCE hInstance, HINSTANCE, LPSTR, int){
//регистрация класса окна в системе
	wnds.style		=CS_HREDRAW + CS_VREDRAW + CS_GLOBALCLASS;
	wnds.lpfnWndProc	=WindowProc;
	wnds.cbClsExtra	=0;
	wnds.cbWndExtra	=0;
	wnds.hInstance	=hInstance;
	wnds.hIcon		=LoadIcon(0, IDI_APPLICATION);
	wnds.hCursor	=LoadCursor(0, IDC_ARROW);
	wnds.hbrBackground=(HBRUSH) 6;
	wnds.lpszMenuName	=0;
	wnds.lpszClassName=ClassName;	//атрибуты структуры окна заполнены
	RegisterClass(&wnds); 		//зарегистрируем класс окна
	Wnd=CreateWindowEx(0, ClassName,
		"Процесс1: Прямоугольники",
		WS_EX_DLGMODALFRAME,
		GetSystemMetrics(SM_CXFULLSCREEN)/2 - SizeWindow,
		GetSystemMetrics(SM_CXFULLSCREEN)/2 - SizeWindow,
		SizeWindow, SizeWindow/2,
		0,0,hInstance,0);	//создадим экземпляр  зарегистрированного класса окна
	
	ShowWindow(Wnd,SW_SHOWNORMAL);	//отобразим окно на экране
	hdc=GetDC(Wnd);			//получим его контекст
	SetTimer(Wnd,1,100,NULL);		//установим таймер
	int Exit=1;

	while(Exit)
	{			//обработка сообщений от окна
		if((Exit=GetMessage(&msg,0,0,0)) )
		{
			TranslateMessage(&msg);
			DispatchMessage(&msg);
		}
	}
	return 0;
}

Второй процесс

#include <windows.h>	//заголовочный файл для win32 приложений
#pragma hdrstop
#define SizeWindow 400	//размер окна

MSG msg;		//сообщение
HDC hdc;		//контекст устройства
HBRUSH hBrush;		//тип кисти
HWND Wnd;		//handle окна
WNDCLASS wnds;		//структура класса окна
char ClassName[255]="Circle";	//имя класса окна

LRESULT CALLBACK WindowProc(HWND hWnd, UINT uMsg, WPARAM wParam, LPARAM lParam){//оконная функция
int x,y,r; //координаты центра и радиус окружности
switch(uMsg)
{
	case WM_DESTROY: 	//выход
		PostQuitMessage(0); return 0;
	case WM_TIMER: 	//таймер
		//генерируем координаты и радиус и рисуем эллипс
		x = rand()%SizeWindow;	y = rand()%SizeWindow;	r = rand()%SizeWindow/4;
		Ellipse(hdc,x-r, y+r,x+r,y-r);
	default: //по умолчанию
		DefWindowProc(hWnd,uMsg,wParam,lParam);
		break;
}
}

int WinMain(HINSTANCE hInstance, HINSTANCE, LPSTR, int){
//регистрация класса окна в системе
	wnds.style		=CS_HREDRAW + CS_VREDRAW + CS_GLOBALCLASS;
	wnds.lpfnWndProc	=WindowProc;
	wnds.cbClsExtra	=0;
	wnds.cbWndExtra	=0;
	wnds.hInstance	=hInstance;
	wnds.hIcon		=LoadIcon(0, IDI_APPLICATION);
	wnds.hCursor	=LoadCursor(0, IDC_ARROW);
	wnds.hbrBackground=(HBRUSH) 6;
	wnds.lpszMenuName	=0;
	wnds.lpszClassName=ClassName;	//атрибуты структуры окна заполнены
	RegisterClass(&wnds); 		//зарегистрируем класс окна
	Wnd=CreateWindowEx(0, ClassName,"Процесс2:Окружности",
		WS_EX_DLGMODALFRAME,
		GetSystemMetrics(SM_CXFULLSCREEN)/2-SizeWindow,GetSystemMetrics(SM_CXFULLSCREEN)/2 - 1.75*SizeWindow,
		SizeWindow, SizeWindow/2,0,0,hInstance,0);			//создадим экземпляр зарегистрированного класса
		
	ShowWindow(Wnd,SW_SHOWNORMAL);	//отобразим окно на экране
	hdc=GetDC(Wnd);			//получим его контекст
	SetTimer(Wnd,1,100,NULL); 	//установим для него таймер
	int Exit=1;
	while(Exit)				//обработка сообщений от окна
	{
		if((Exit=GetMessage(&msg,0,0,0)) )
		{
		TranslateMessage(&msg);
		DispatchMessage(&msg);
		}
	}
	return 0;
}

Основной процесс

#include <windows.h>	//заголовочный файл для win32 приложений
#include <string.h>		//заголовочный файл для работы со строками
#include <stdio.h>		//заголовочный файл для ввода-вывода
//идентификаторы, используемые в программе
#define ID_PROCESS 3         
#define ID_KILLPROC 2
#define ID_EXIT 4
#define ID_HELP 1
#define PROCMAX 2
#define MAINMENU 1
#define IDI_ICON1 1
//прототип оконной функции
LRESULT CALLBACK WindowFunc(HWND,UINT,WPARAM,LPARAM);

char szWinName[] = "main"; 	//имя окна
char str[255];		  	//буфер	
int maxX,maxY;			//максимальные значения Х и У
int X=0, Y=0;
int procnum = 0;			//номер процесса

HDC memdc;				//контекст окна
HBITMAP hbit;				//handle картинки
HBRUSH hbrush;			//тип кисти
PROCESS_INFORMATION pinfo[PROCMAX]; 	//массив структур информации 
							//о процессах
//главная функция приложения
int WINAPI WinMain( HINSTANCE hThisInst, HINSTANCE hPrevinst, LPSTR lpszArgs, int nWinMode)
{
	 HWND hwnd;		//handle окна
	 MSG msg;		//сообщение
	 WNDCLASS wcl; 	//класс окна
	 HANDLE hAccel=NULL;	//акселераторы

	//регистрируем новый класс окна в системе
	 wcl.hInstance		 = hThisInst;
	 wcl.lpszClassName 		 = szWinName;
	 wcl.lpfnWndProc	 	 = WindowFunc;
	 wcl.style 			 = 0;
	 wcl.hIcon 		 	 =LoadIcon(NULL, MAKEINTRESOURCE(IDI_ICON1));
	 wcl.hCursor		 	 = LoadCursor(NULL,IDC_ARROW);
	 wcl.lpszMenuName	 	 = (LPSTR)MAKEINTRESOURCE(MAINMENU);
	 wcl.cbClsExtra	 	 = 0;
	 wcl.cbWndExtra	 	 = 0;
	 wcl.hbrBackground 		 = (HBRUSH)GetStockObject(WHITE_BRUSH);

	 if(!RegisterClass(&wcl)) return 0; //класс окна зарегистрирован
	//создадим экземпляр нового класса
	hwnd = CreateWindow(szWinName,
		"Лабораторная работа №1, Вариант 1, ПП",
		WS_OVERLAPPEDWINDOW,GetSystemMetrics(SM_CXFULLSCREEN)/2-400,GetSystemMetrics(SM_CXFULLSCREEN)/2-200,450,150,//150,370,450,150, 
		HWND_DESKTOP, NULL, hThisInst, NULL);

	ShowWindow(hwnd,nWinMode);	UpdateWindow(hwnd); //отобразим его на экране

	while(GetMessage(&msg,NULL,0,0)) //обработка сообщений от окна
	{
		if(!TranslateAccelerator(hwnd,(HACCEL)hAccel,&msg))
		{
			TranslateMessage(&msg);	DispatchMessage(&msg);
		}
	 }
	return msg.wParam;
}

//оконная функция
LRESULT CALLBACK WindowFunc(HWND hwnd, UINT message,	WPARAM wParam,	LPARAM lParam)
{
	HDC hdc;			//контекст
	PAINTSTRUCT paintstruct;	//структура для рисования
	TEXTMETRIC tm;		
	STARTUPINFO startin;	//структура для запуска процессов

	switch(message)
	{
		case WM_CREATE: //если окно создаётся, заполним область вывода белым цветом
			maxX = GetSystemMetrics(SM_CXSCREEN);
			maxY = GetSystemMetrics(SM_CYSCREEN);
			hdc = GetDC(hwnd);
			memdc = CreateCompatibleDC(hdc);
			hbit = CreateCompatibleBitmap(hdc,maxX,maxY);
			SelectObject(memdc,hbit);
			hbrush = (HBRUSH)GetStockObject(WHITE_BRUSH);
			SelectObject(memdc,hbrush);
			PatBlt(memdc,0,0,maxX,maxY,PATCOPY);
			ReleaseDC(hwnd,hdc);
			break;
		case WM_COMMAND: //если нажата одна из опций меню
			switch (LOWORD (wParam))
			{
				case ID_PROCESS: //открыть процесс
				{	
					if(procnum==PROCMAX) //если их два, то больше нельзя
					{
						MessageBox(hwnd,"Запущены оба процесса", "Ошибка", MB_OK);
						break;
					};
					
					char TestName[]="PP_lab1_process .exe"; //здесь создаётся имя для запуска
					TestName[15]=procnum+49;
					//заполним структуру STARTUPINFO
					startin.cb          = sizeof(STARTUPINFO);
					startin.lpReserved  = NULL;
					startin.lpDesktop   = NULL;
					startin.lpTitle     = NULL;
					startin.dwFlags     = STARTF_USESHOWWINDOW;
					startin.cbReserved2 = 0;
					startin.lpReserved2 = NULL;
					startin.wShowWindow = SW_SHOWNORMAL;
					//запускаем новый процесс
					if (CreateProcess(NULL, TestName ,NULL,NULL,FALSE,0,
						NULL,NULL,&startin, &(pinfo[procnum])))
             	  	{ 	  
						//вывод в главное окно, что процесс создан
						GetTextMetrics(memdc,&tm);
						sprintf(str,"Процесс %d создан",procnum);
						TextOut(memdc,X,Y,str,strlen(str));
						Y = Y + tm.tmHeight+tm.tmExternalLeading;
						InvalidateRect(hwnd,NULL,1);
						//перерисуем окно
						procnum++;
                 	} 
					else MessageBox(hwnd,"Не найдена тестовая программа!","Ошибка",MB_OK);
				
				} 
				break;

				case ID_KILLPROC: //закрыть процесс
					if(procnum) procnum--; //декремент количества процессов
					else
					{ //если нечего закрывать
						MessageBox(hwnd,"Все процессы закрыты","Ошибка",MB_OK);
						break;	
					}
					GetTextMetrics(memdc,&tm);
					//функция завершает процесс
					TerminateProcess(pinfo[procnum].hProcess,0);
					//вывод в главное окно, что процесс завершён
					sprintf(str,"Процесс %d завершен",procnum);
					TextOut(memdc,X,Y,str,strlen(str));
					Y = Y+tm.tmHeight+tm.tmExternalLeading;
                  	InvalidateRect(hwnd,NULL,1);
					break;

					case ID_EXIT: //Выход
					{
						TerminateProcess(pinfo[0].hProcess,0);TerminateProcess(pinfo[1].hProcess,0);
						DeleteDC(memdc);	PostQuitMessage(0);
					}
					break;
			} break;
		case WM_PAINT: //перерисовка окна
			hdc = BeginPaint(hwnd,&paintstruct);
			BitBlt(hdc,0,0,maxX,maxY,memdc,0,0,SRCCOPY);
			EndPaint(hwnd,&paintstruct);
			break;
		case WM_DESTROY: //если нажата кнопка, закрыть
			DeleteDC(memdc);
			PostQuitMessage(0);
			break;
		default: //	по умолчанию
			return DefWindowProc(hwnd,message,wParam,lParam);
	}
	return 0;
}

Результат работы программы:



Исходный код программы:

#include <windows.h>
#include <time.h>              // получение первого случайного числа
#include <iostream>          // ввод-вывод
#include <conio.h>             // для включения ожидания ввода клавиши
using namespace std;
     
#define N 10                   // степень многочлена
double x;                      // значение переменной

struct arg                     // структура для передачи параметров
{
	int l, r;                     // нижний и верхний номера 2х2=матрицы
	double p, q;                  // коэффициенты первой строки матрицы
};

double a[2*N+2];                    // коэффициенты многочлена
DWORD WINAPI prod(void* s)     // функция потока
{
		int i, l=((arg *)s) -> l, r=((arg *)s) -> r;
		Sleep(rand()%1000);           // случайная задержка
		if (l == r)
		{
			((arg *)s) -> p = x;    // установка
			((arg *)s) -> q = a[l];  // коэффициентов
		}
		else
		{
			arg *r1 = new arg, *r2 = new arg;
			HANDLE H[2];                                   // дескрипторы потоков
			r1 -> l = l;				r1 -> r = (l + r + 1)/2 - 1; //установка границ
			r2 -> l = (l + r + 1)/2;	r2 -> r = r;
			H[0] = CreateThread(0,0,prod, (void *)r1,0,0); // порождение
			H[1] = CreateThread(0,0,prod, (void *)r2,0,0);  // потоков
			for (i = 0; i < 2; i++)  WaitForSingleObject(H,INFINITE); // ожидание выполнения потоков
			((arg *)s) -> p = (r1 -> p)*(r2 -> p); //p1*p2
			((arg *)s) -> q = (r1 -> p)*(r2 -> q)+(r1 -> q);//p1*q2+q1
			delete r1; delete r2;
		}
		return 1;
}

double fact(double f)
{
	if(f==0||f==1) return(1);
	return(f*fact(f-1));
}

void main()
{
	int i; double w=0, z;
	srand(time(NULL));//Включение генератора с.ч.
	for (i=0; i <=2*N+1; i=i+2) a[i] = 0;  // установка коэффициентов перед x с чётной степенью
	for (i=0; i <=N; i++) a[2*i+1] = pow(-1.0,(i))/fact(2*i+1);  // установка коэффициентов перед x С нечётной степенью
 
	arg t;                        // объявление структуры параметров
	for (x = 1; x <10; x++) //перебор значений х
	{
		t.l = 0; t.r = 2*N+1;       // границы массива матриц
		prod(&t);  // вызов подпрограммы
  		cout <<"x=" << x << " Polynom value = " << t.q<<endl; // вывод
		z = 0;
		for (i = 0; i <= N; i++)                    // цикл для проверки
		//вычисление правой части выражения
		{	z+=pow(-1.0,i)*pow(x,2*i+1)/fact(2*i+1);	}
		cout <<"\tsin(x)=\t\t" <<sin(x)<<"\n\tRight part=\t"<<z<<endl; // вывод значения для проверки
		getch();                             // ожидание нажатия клавиши
	}

}

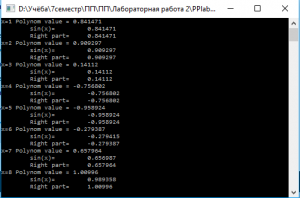
[I]Результат работы программы:

Математика Формулы

Решение дифференциального уравнения первого порядка.

Найти общее решение дифференциального уравнения первого порядка.

Решение.
Положим , тогда

Получили уравнение с разделяющимися переменными.
Разделим переменные и проинтегрируем.

Т.к. y=ux
- Общее решение дифференциального уравнения.

Педагогическая валеология

Часто методы выявления знаний в школе не адекватны

психофизиологическим характеристикам учащихся

Педагогическая валеология

Циклические колебания интенсивности биологических процессов и явлений — это:
биологические ритмы

Педагогическая валеология

Центральное место в системе профилактических мероприятий занимает разработка

оптимальных режимов обучения

Педагогическая валеология

Цель валеологического центра в образовательном учреждении

реабилитация субъектов образовательного процесса

Педагогическая валеология

Формы человеческой (индивидуальной и групповой) жизнедеятельности, типичные для исторически конкретных социальных отношений, — это:

образ жизни